Theory of high-efficiency adiabatic frequency conversion in coupled microrings
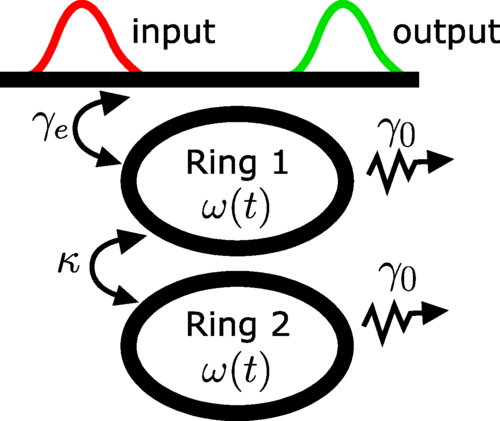
Adiabatic frequency conversion (AFC) in microring resonators is a promising alternative for integrated, tunable frequency shifting of optical signals. However, the efficiency of AFC in a single-ring resonator is limited to below 80% for symmetric input pulses with a single peak. This is the consequence of a poor match between the pulse shape and the ring's impulse response. To overcome this limitation, we propose inducing AFC over two coupled rings rather than a single ring. We analyze the process's efficiency using temporal coupled mode theory (TCMT). We show that two-ring AFC can attain an efficiency of 97% in the limit of negligible intrinsic ring loss. To explain this higher AFC efficiency, we analyze two-ring AFC as a linear operator of rank two in the vector space of finite-energy pulses. We represent the AFC operator as a 2×2 matrix and examine its singular value decomposition. In this way we analyze the dependence of the two-ring AFC efficiency on the input pulse shape and the TCMT parameters.